What is ECC
Elliptic Curve Cryptography (ECC) is an asymmetric cryptographic algorithm that is gaining popularity due to its strong security and smaller key sizes compared to other common algorithms like RSA.
It is especially suitable for key exchange and is often combined with symmetric algorithms like Advanced Encryption Standard (AES) to secure information transmission. ECC is widely used in technologies and services like TLS and Signal.
How Does ECC Work
In essence, ECC works by deriving a third point from two known points on a curve. The key components of the algorithm are:
- An elliptic curve defined by a cubic equation in this form: y2 = x3 + ax + b. The curve is symmetric across the x-axis.
- A random starting point,
G, on the curve, which is agreed upon by both parties.
The most difficult part to grasp is how a third point is derived. This is achieved through what is called scalar multiplication.
Scalar Multiplication
Let's say there is a point H on an elliptic curve, and H = G + G + G + ..., then H is a scalar multiple of G. Mathmatically, we express H as:
H = a・G
Where a is an integer scalar.
Scalar multiplication is entirely different from traditional arithmetic addition. If
G = (0, 1), we cannot compute2Gas:❌
2G = (0+0, 1+1) = (0, 2)
Instead, we use a special geometric method of point addition to derive the new point. Here is an example using the curve y2 = x3 - x + 1 and the starting point G = (0, 1) to compute 3G.
Step 1: Derive 2G
Normally, to add two points, we draw a line between them, find the third point of intersection with the curve, and reflect it across the x-axis.
When calculating 2G = G + G, we draw the tangent line at G (since the two points are the same), find its intersection with the curve, and reflect that point to get 2G.
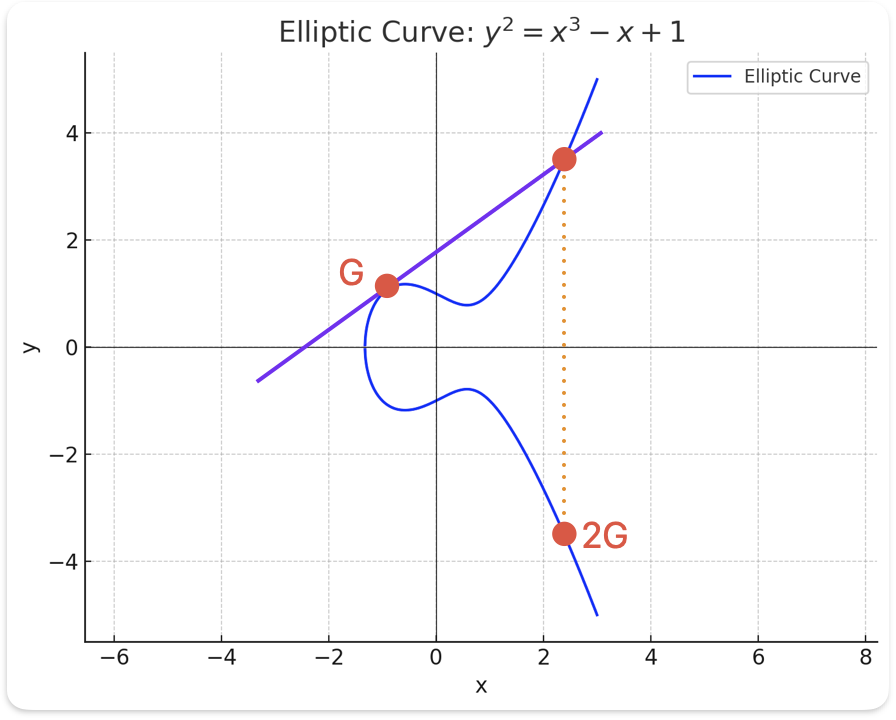
Step 2: Derive 3G
Now, draw a line through G and 2G, find the third point of intersection with the curve, and reflect it across the x-axis to obtain 3G.
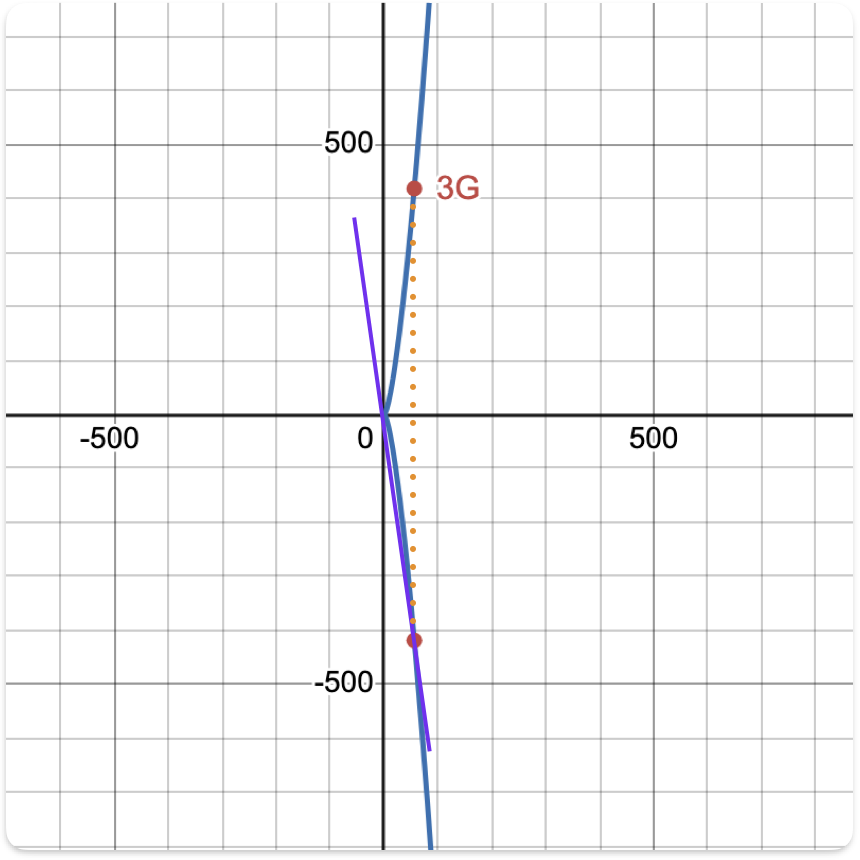
(Since 3G = (56, 419), the graph is zoomed out to include all relevant
points)
A Complete Example
Now that we understand how scalar multiplication works, we can walk through how ECC is used to generate keys and create a shared secret for secure message transmission.
Step 1: Agree on a Curve and Point
Suppose Alice and Bob want to exchange keys using ECC. First, they agree on the elliptic curve and a base point on the curve, G.
Step 2: Choose Private Keys
Alice and Bob each select a random integer, a and b, as their private keys.
Step 3: Compute Public Keys
They then compute their public keys, A and B, using scalar multiplication:
A = a・G
B = b・GStep 4: Derive a Shared Secret
Each party uses their private key and the other’s public key to compute the shared secret:
S = a・B = b・A = a・b・G
This works because of the associative property of ECC point multiplication.
Step 5: Derive a Symmetric Key
Since ECC is typically used for key exchange, not for encrypting actual messages, the shared point S is passed through a Key Derivation Function (KDF)—such as SHA-256—to derive a symmetric key:
Key = KDF(Sx)
Where Sx is the x-coordinate of the shared point.
Alice and Bob now use the derived symmetric key with a fast symmetric algorithm like AES to encrypt and decrypt their actual messages.
Why Is ECC Popular
Strong Security
ECC’s security relies on a difficult mathematical problem called the Elliptic Curve Discrete Logarithm Problem (ECDLP), which asks:
Given a point
Gand another pointa・G, can you determinea?
The answer is: not feasibly. While scalar multiplication is easy, reversing it to recover the private key is computationally infeasible, even with powerful hardware.
High Performance
ECC can achieve the same level of security as RSA but with much smaller key sizes.
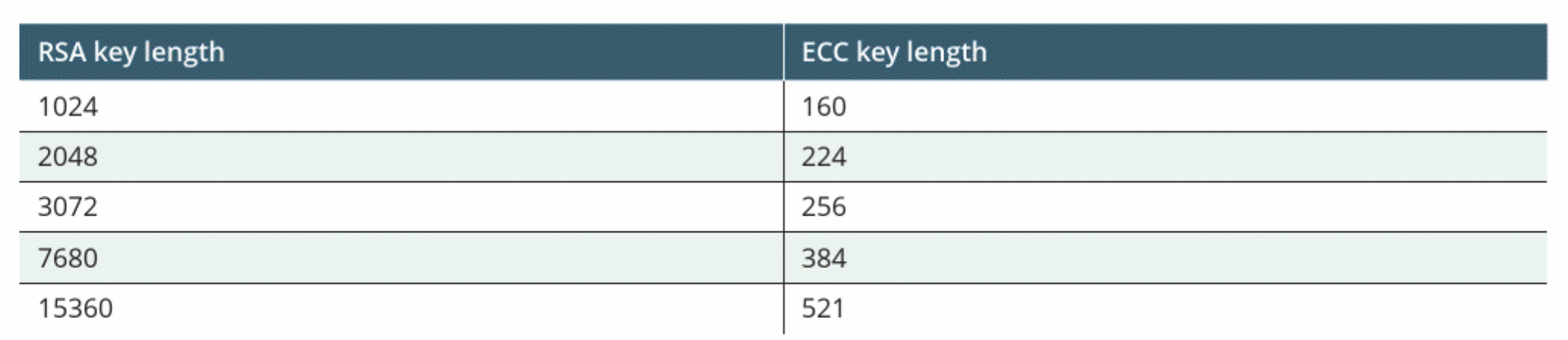
ECC vs. RSA key lengths for same security level. (Image source: Ciampa, M. (2024). Comptia+ security+ guide to network fundamentals. Cengage.)
This makes ECC faster and less resource-intensive, which is especially important for mobile devices and low-power systems.
Conclusion
Elliptic Curve Cryptography is one of the most widely used asymmetric encryption methods today due to its strong security and high efficiency. Major operating systems, web browsers, and secure messaging apps rely on ECC—and it is especially valuable for resource-constrained devices like smartphones, wearables, and IoT sensors.